序

很久没有更新文章了……最近体检发现自己竟然重了8kg，年初定下的今年长肉目标竟然在年中就实现了～，不过体检也发现了一些毛病，感觉下半年需要控制体重和养生了……

最近自己也一直没有闲着，除了工作之外，依然在坚持学习一些东西。最近随着工作中针对特定功能的不断深入，越发觉得数据结构、算法以及设计模式太重要了，将工作中的某些功能进行抽象，然后将抽象出的东西进行建模，再利用通用的数据结构和算法去解决问题，是我最近能够清晰悟出来的道理。

所以接下来我们来聊聊算法，后续考虑会每隔一段时间写一篇关于数据结构和算法的文章，今天主要来看看字符串匹配算法中的单模式串匹配算法。

BF和RK算法

在介绍算法之前，我们还是先来说一说两个概念，主串和模式串，这两个概念说来也不难理解，下面我们举个例子：

假设有一个字符串A为abcdef，我们想看一下字符串B即abc是否存在于字符串A中，那么字符串A就是主串，而字符串B就是模式串。

BF算法

说到字符串匹配，我们常见的解决方式可能就是比较简单暴力的BF算法了，BF算法中的BF是Brute Force的缩写，中文叫暴力匹配算法，也叫朴素匹配算法，这种算法操作比较简单，同时也很好理解，但是性能也不高。

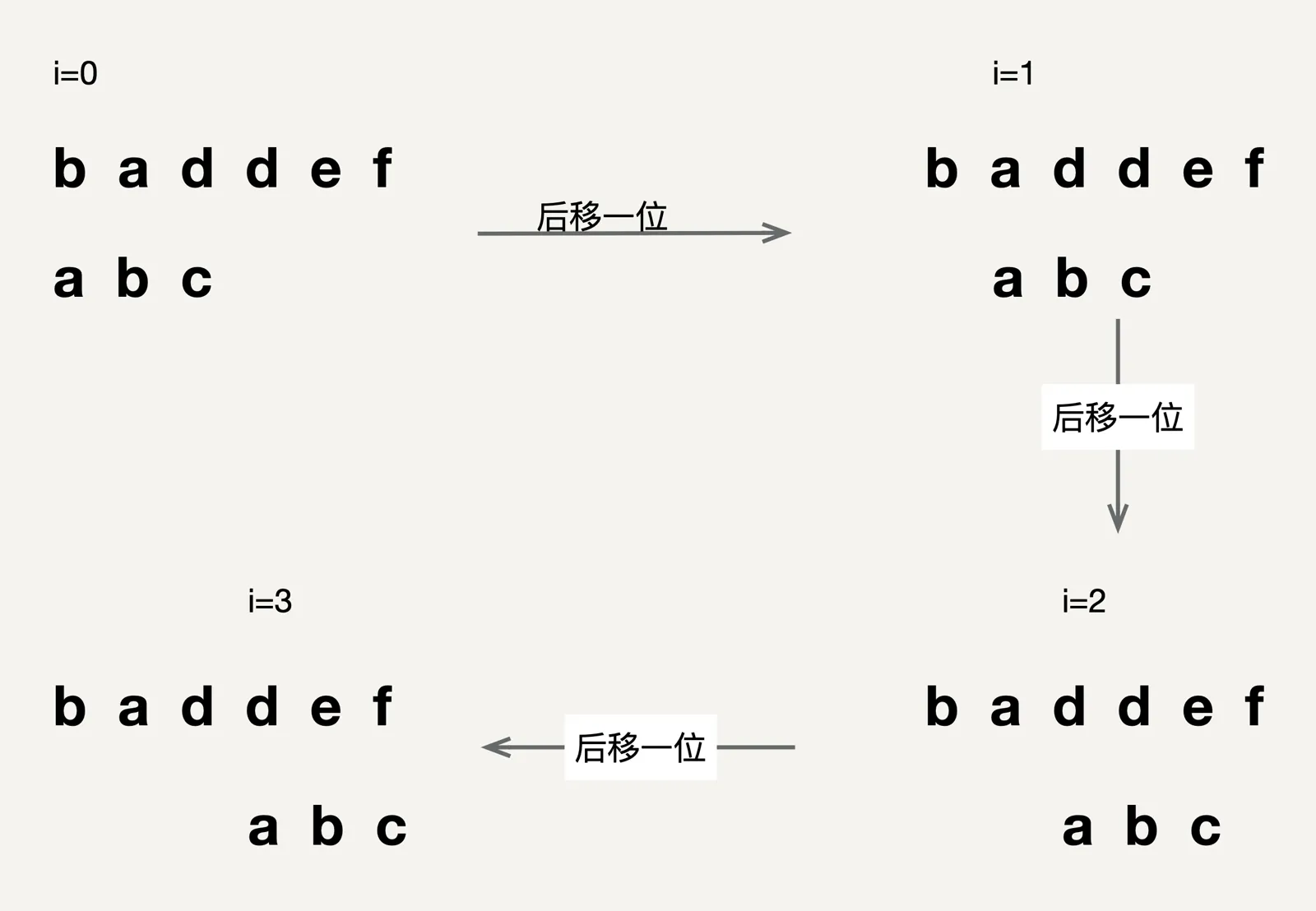
它的思想用一句话来说就是，我们在主串中，检查起始位置分别是0、1、2、3、4……n-m且长度为m的n-m+1个子串，看有没有跟模式串匹配的（注：文中n表示主串的长度，m表示模式串的长度）。

具体实现如图：

从上面的例子以及图示可以知道，BF算法中，主串和模式串的匹配规则是，模式串每一次只会向右移动一位长度，然后从头开始与主串进行对比，假设极端情况下，主串是aaa……aab，而模式串是aaaab，模式串每一次对比的长度都是模式串长度m减1，而最终需要对比到主串的最后一个子串的时候，才会对比成功，此时对比的子串个数为n-m+1，所以最终BF算法在极端情况下的时间复杂度为O(n*m)，可以看出在极端条件下的时间复杂度还是比较高的。

虽然在某些条件下，BF算法的时间复杂度比较高，但是在大部分条件下，BF算法依然还是一个比较受欢迎的算法，一来该算法实现起来较为容易，简单暴力匹配即可，正是如此，所以写起来也是十分方便，产生的bug可能性也会大大降低；二来我们正常开发条件下的字符串匹配，遇到的字符串长度都不会很长（除了专门针对文章的字符串匹配，比如敏感字段过滤等等，那么这样的算法明显是不行的），所以从实用角度来看，该算法不失为一个好算法。

RK算法

RK算法，全称叫做Rabin-Karp算法，它是由Rabin和Karp发明的，故以二者名字来命名该算法。

该算法和上面说到的BF算法是没有太多的差别，所以总的来说就是BF算法的升级版本。

从上面关于BF算法的介绍可知，模式串每一次和主串中的子串对比的时候，模式串都需要从头开始往后对比，导致极端情况下时间复杂度会很高，所以我们能不能不是每一次都从头开始对比呢？答案是能，而且方法很多，RK算法就是其中一种，RK算法考虑当模式串和主串中的子串开始匹配之前，先做一件事–将当前子串的哈希值和模式串的哈希值拿出来先比对一下，看看模式串和子串的哈希值是否相等，如果相等，那么才开始进行字符串匹配工作。

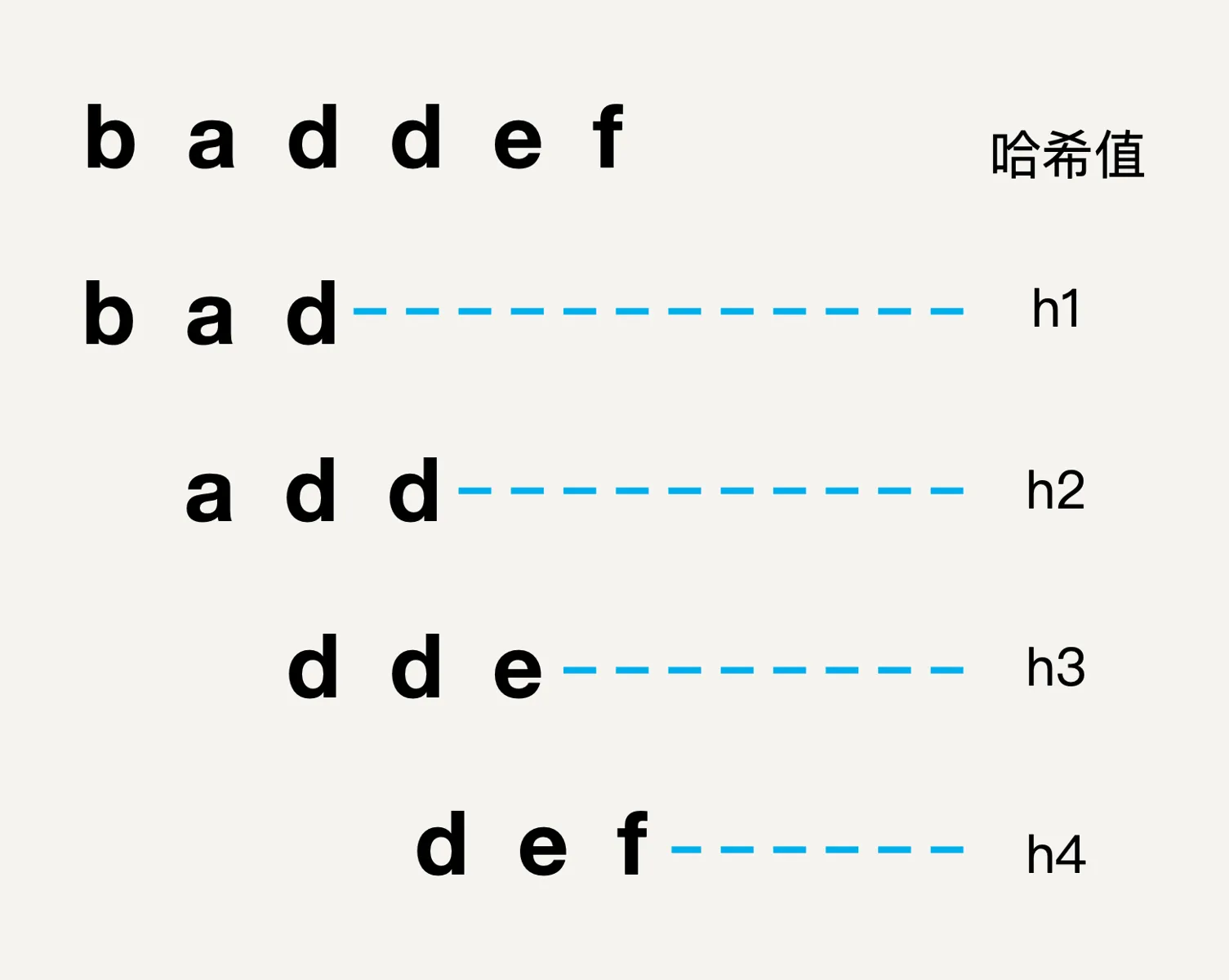
因为两个字符串如果相同，那么哈希值也一定是一样的，而两个字符串的哈希值如果一样，那么两个字符串可能相同，所以依靠这样的方式，可以大大节省字符串的匹配时间，提高匹配效率。具体如下图所示：

从图中可以看出，我们对主串的所有的和模式串相同的子串都进行哈希求值，然后当模式串进行匹配的时候就可以预先进行哈希值对比，当哈希值相同的时候才进行字符串比对，达到节省时间的目的。

但是，该如何获取所有子串的哈希值呢？换句话说，该如何设计哈希算法呢？如果按照正常逻辑，我们需要遍历子串中的每一个字符，然后计算得到该子串的哈希值，这样做的话，即使子串与模式串的对比效率提高了，但是由于获取所有子串哈希值还是浪费了很多时间，所以导致算法整体效率并没有多大的提高，所以需要考虑使用一种非常高效的方式来获取这些子串的哈希值。

经过观察，我们可以发现，两个相邻子串之间其实是有联系的，它们之间除了第一个子串的头部和第二个子串的尾部可能不同之外，其他字符串都是相同的，举个例子，上面主串的第一个子串bad和第二个子串add，它们之间的相同的字符串部分是ad，不同字符是第一个子串的b以及第二个子串的d。从这个角度来看，我们就可以利用特定算法，依据第一个子串的哈希值，来推导第二个子串哈希值。

假设现在字符串中只有a~z这26个小写英文字母，那么我们就可以使用26进制来表示一个字符串。我们把a~z这26个字母，映射到0~25这26个数字中，这样a就是0，b就是1，以此类推。

这样上面主串中的子串我们就可以使用26进制来进行描述，例如子串bad使用26进制进行描述就是bad=1*26*26+0*26+3*1，而add使用26进制进行描述就是add=0*26*26+3*26+3*1，我们可以利用bad来推导add，add=(bad-1*26*26)*26+3*1，即add=bad-b+d，可能到这里你还是有一点点懵懵懂懂，那么我们再抽象一下：

假设主串中相邻两个子串分别为s[i-1,i+m-2]和s[i,i+m-1]，其中i表示子串在主串中的起始位置，子串长度都为m。那么我们该如何表示两个子串的哈希值呢？

设h[i-1]表示子串s[i-1,i+m-2]的哈希值，而h[i]表示子串s[i,i+m-1]的哈希值，所以这两个哈希值之间的关系如下：

1
2
3
4

h[i-1] = 26^m-1 * (s[i-1] - a) + 26^m-2 * (s[i] - a) + …… + 26^0 * (s[i+m-2] - a)
h[i] =                           26^m-1 * (s[i] - a) + …… + 26^1 * (s[i+m-2] - a) + 26^0 * (s[i+m-1] - a)

h[i] = 26 * (h[i-1] - 26^m-1 * (s[i-1] - a)) + 26^0 * (s[i+m-1] - a)

针对26^m-1部分，可以考虑使用查表法，将常用的26^0、26^1、26^2……26^m-1存储在一个长度为m的数组中，当需要计算26的次方时，就可以直接通过查表法拿到相应的数据，达到加速查询的效果。

从上面的计算哈希值的算法来看，有一个问题这里需要说明一下，如果计算的哈希值很大，超过了计算机整型数据可以表示的范围，那么该如何解决？

由于上面的讨论都是在没有哈希冲突的前提下提出的，所以这里可以考虑放宽条件，即允许一定程度的哈希冲突，让计算的哈希值存在于整型范围内，这样上面的算法就需要重新设计，假设字符串的范围依然是那26个英文字母，那么可以考虑每一个字母对应一个数字，例如a对应1，b对应2，计算字符串子串哈希值的时候，仅仅将各个字母进行相加，得到的结果就是哈希值。当然，如果觉得这样的方式计算的冲突过多，还可以考虑将这26个英文字母不是对应任意数字，而是对应26个素数，以此来降低哈希冲突率。

RK算法针对哈希算法的设计主要就是要注意避免出现大量的哈希冲突，因为如果冲突过多，会导致算法时间复杂度直线上升，导致最终复杂度逼近BF算法。

BM算法

聊完两种简单的字符串匹配算法之后，就需要过渡到真正的比较趋近于工业级范围的字符串匹配算法，也就是我们接下来聊的BM算法。

BM算法，全称Boyer-Moore算法，和RK算法的名字来源相同，该算法是由Bob Boyer和J Strother Moore设计于1977年，是一个非常高效的字符串匹配算法，但是相对于它高效的字符串匹配，它背后的算法实现理解起来将会十分复杂，需要耐心推导。

核心思想

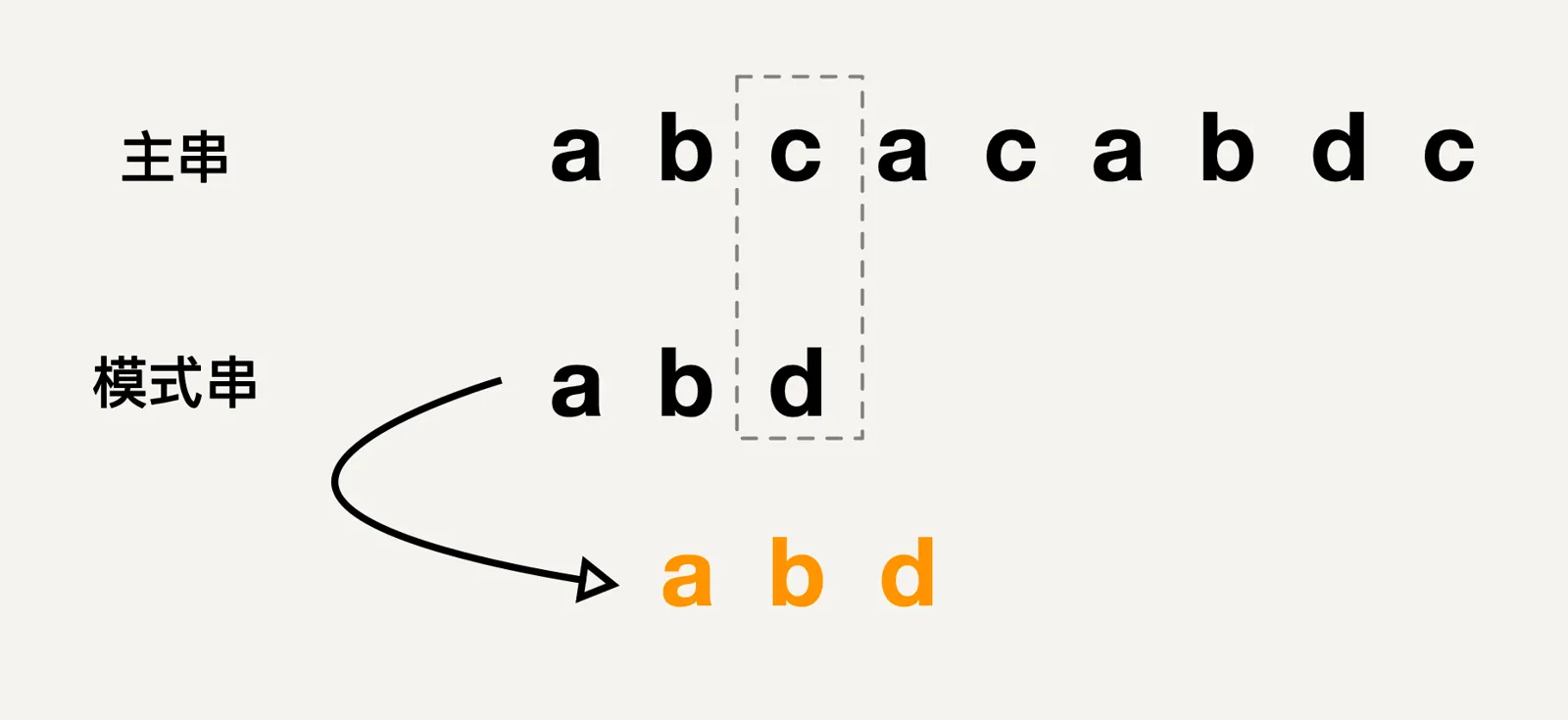
传统的字符串匹配算法在遇到字符串不匹配的时候，是需要将模式串匹配主串的位置向后移动一位之后，再从模式串的开头位置进行对比，如下图所示：

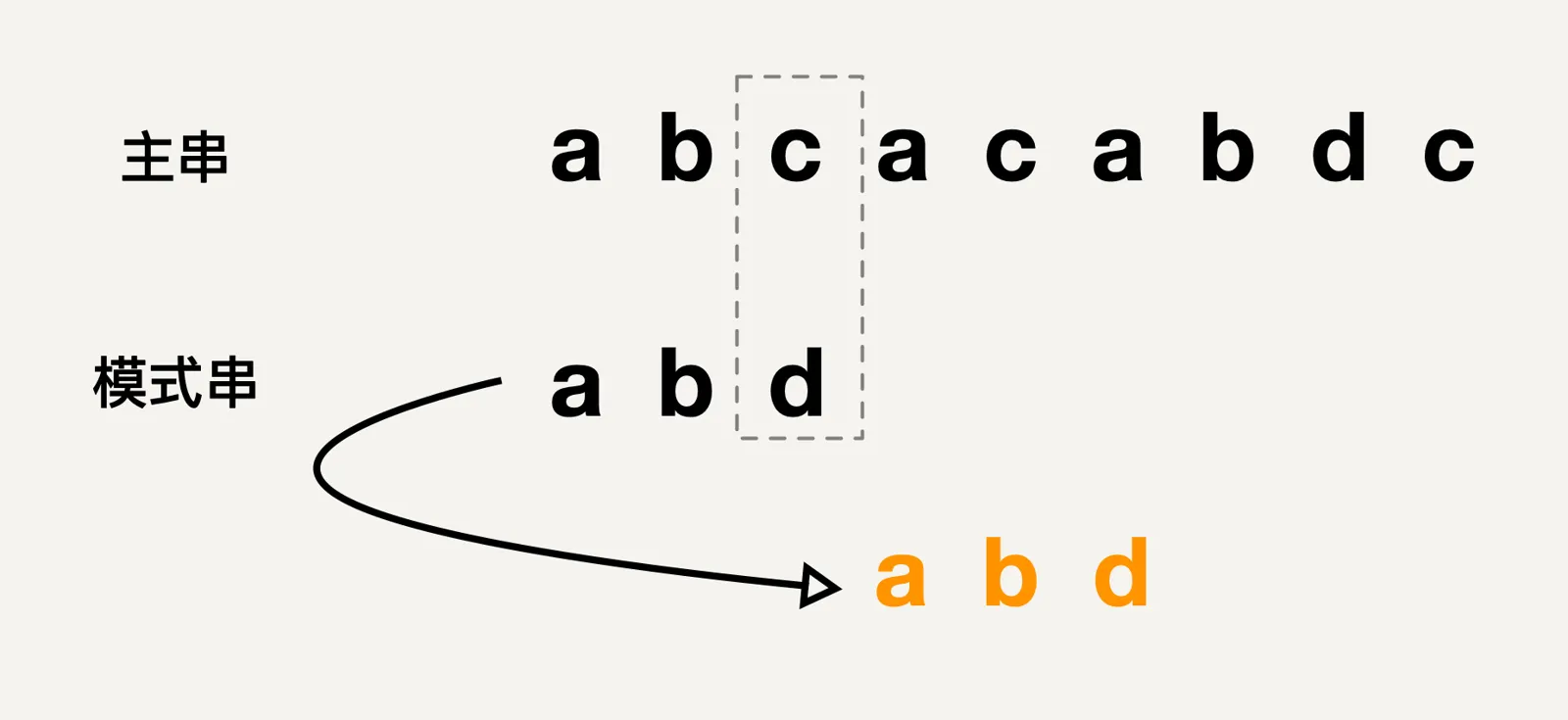
但是上面的方式其实是比较低效的，例如上图中，我们知道模式串中是不存在字符c的，但是却还要每一次向右移动一步来进行字符串匹配，所以能不能考虑一次移动多位，比如上图中将模式串移动到主串第一个c对应的位置的后面一位，然后再开始进行匹配？如下图所示：

从上图有一种感觉，仿佛冥冥中有一种规律，能够在满足一定条件下，将模式串往后多滑动好几位，以此来提高匹配效率。

今天说的BM算法其本质上就是通过找寻这种规律，通过这种规律，在模式串和主串匹配的过程中，当模式串与主串不匹配的时候，能够跳过一些一定不会匹配的情况，将模式串多往后滑动几位。

两个规则

BM算法的核心其实就是找规律，主要包含的就是坏字符规则和好后缀规则，下面依次来看看这两个规则的推导过程。

坏字符规则

在传统的字符串匹配中，我们一般是按照从前往后的匹配顺序，依次对比主串和模式串中的字符，当遇到不匹配的时候就直接让模式串整体向后移动一位。

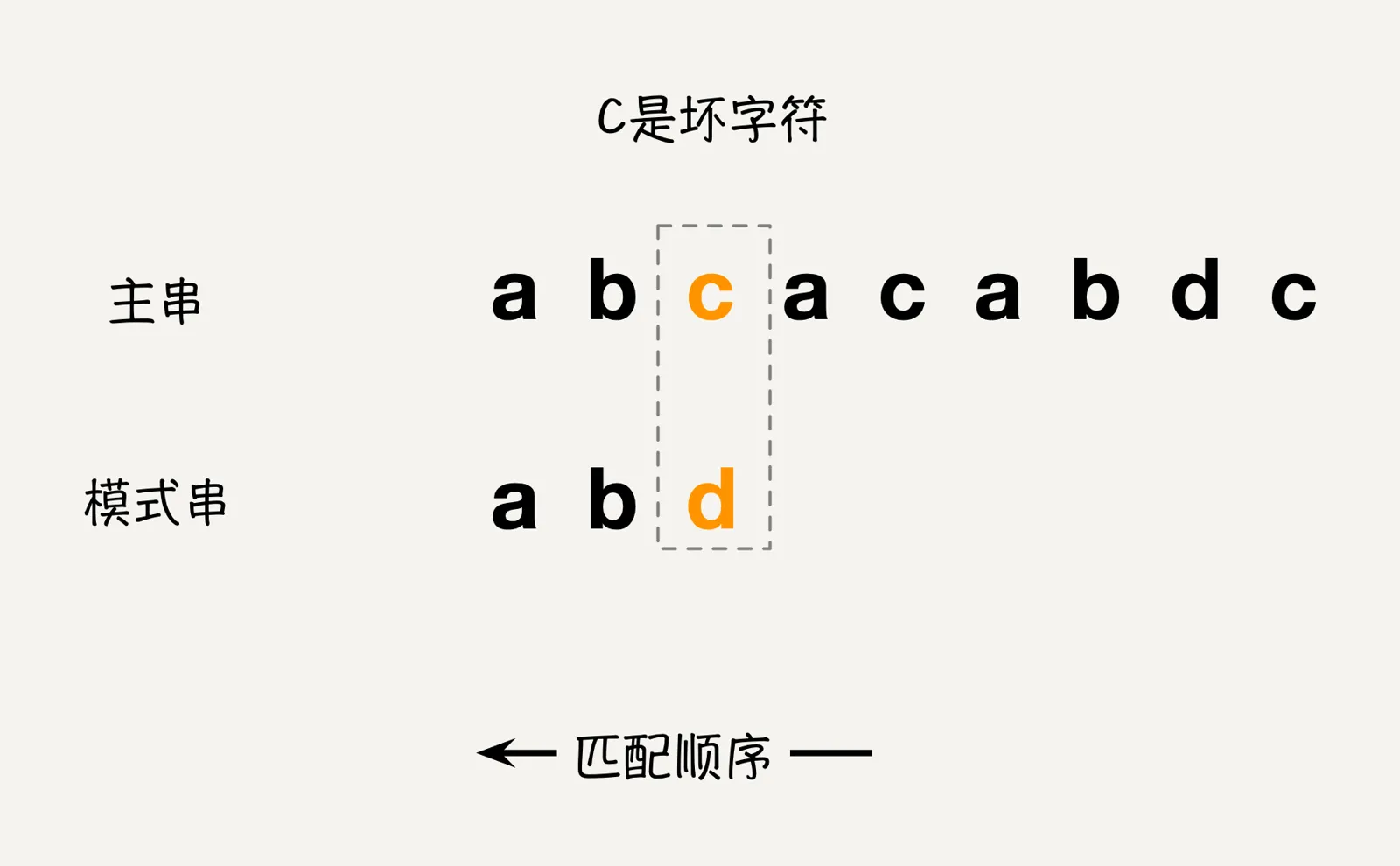
而坏字符规则的匹配顺序和传统规则相反，它是按照从后往前的匹配顺序，当发现某个字符没法进行匹配的时候，就把没有匹配的字符叫做坏字符（注意：这里的坏字符指的是主串中的字符）。

找到坏字符之后，我们拿着这个坏字符c在模式串中进行查找，查看该坏字符是否存在于模式串中，如果存在，那么找到其中模式串索引对应的值的最大值（也就是拿着坏字符，从模式串对应的坏字符位置p开始，从右往左匹配时，能够第一个匹配到的字符对应的索引位置q）；如果坏字符不存在，那么将q值记为-1，模式串向右移动的位置就是模式串对应的坏字符位置p减去q。

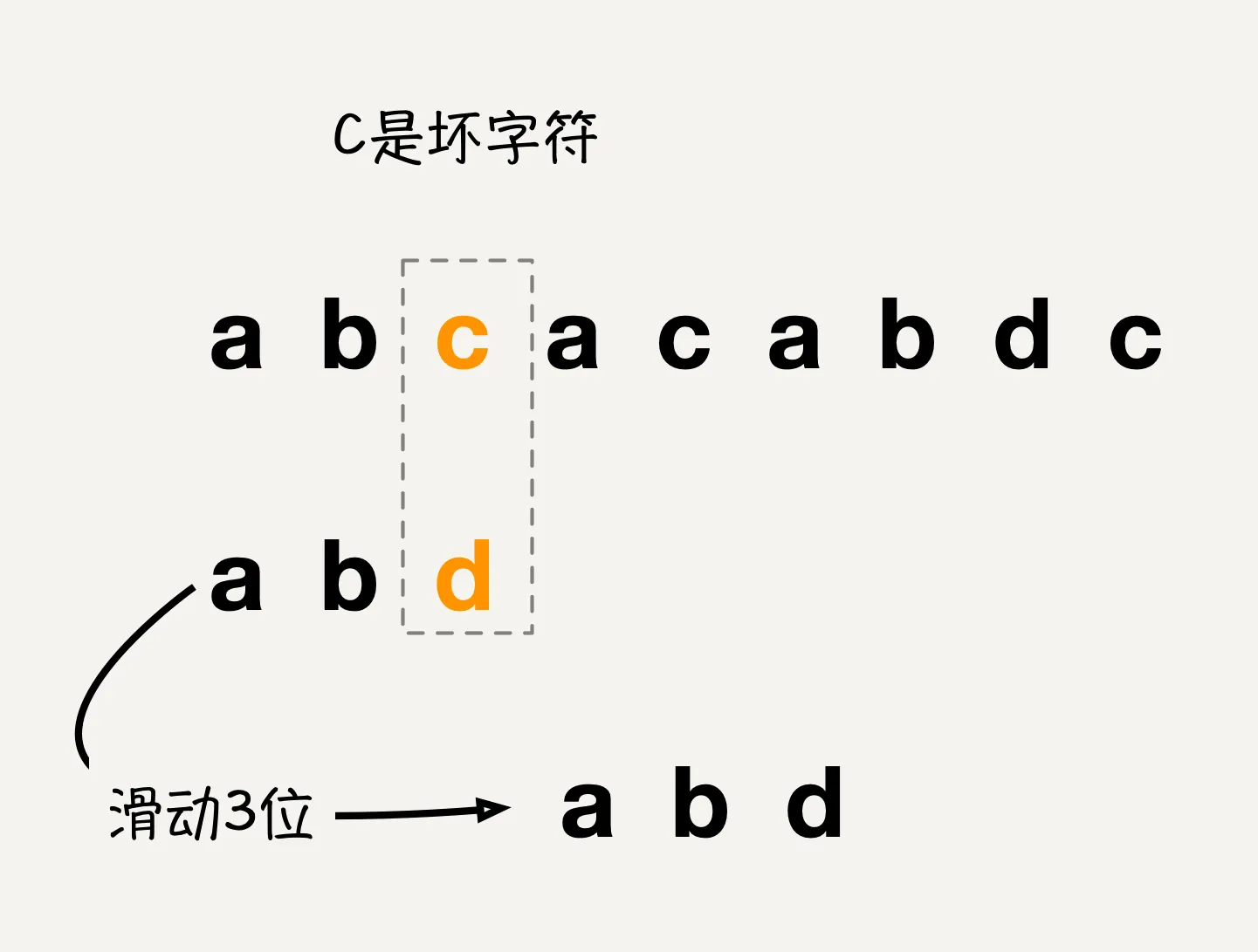
举个例子，如上图所示，当主串和模式串进行匹配的时候，按照从右向左的匹配规则，应该是主串中的字符c和模式串中的字符d进行匹配，因为没有匹配到，所以记录下该坏字符对应的模式串位置p的值为2，然后拿着坏字符c从p位置开始，从右向左进行匹配，匹配到模式串结束，发现模式串中不存在字符c，此时采用q的默认值-1，模式串相对主串向右移动p-q的位置，也就是移动2-(-1)=3位。如图：

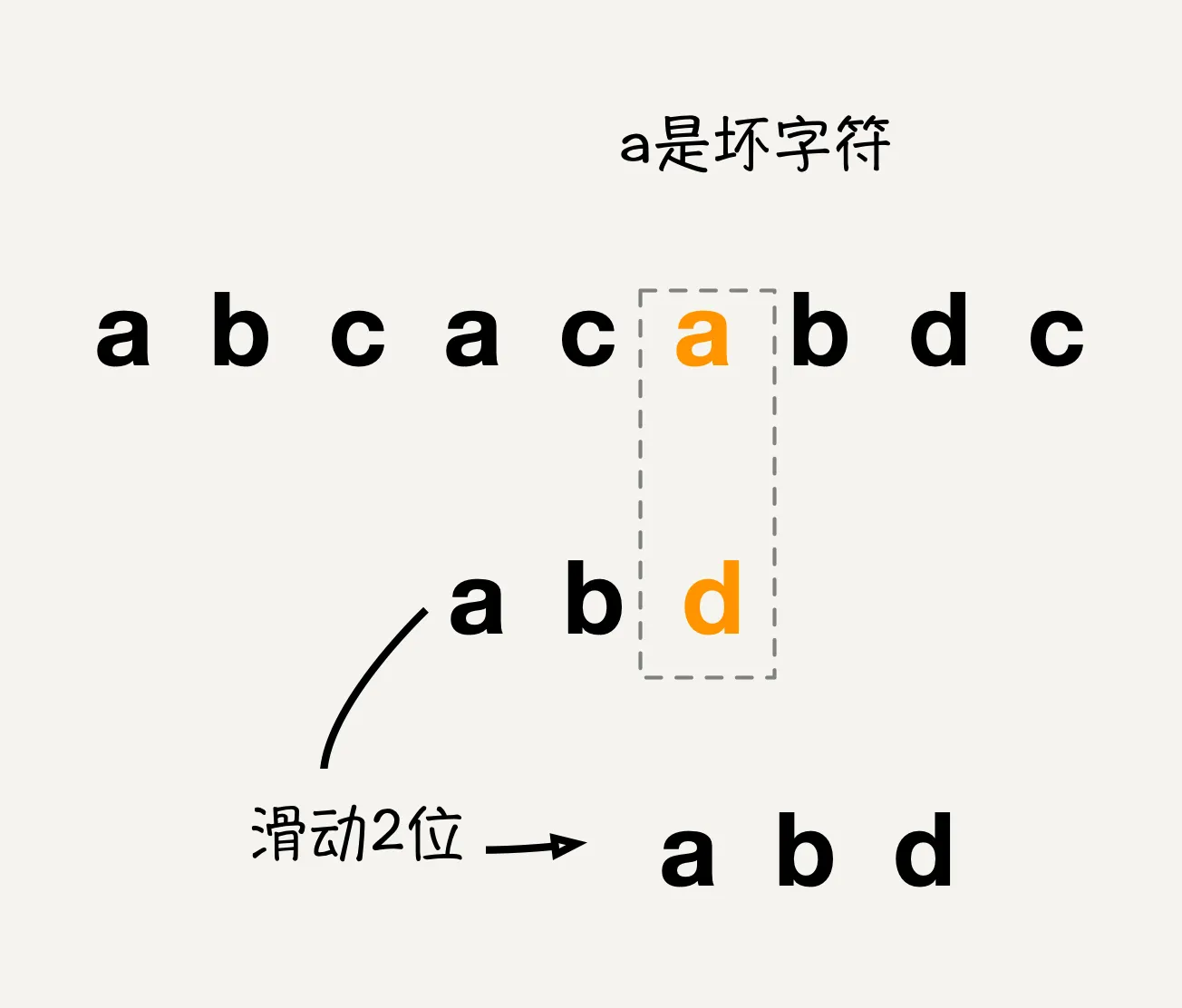
在模式串移动之后，模式串仍然从后往前和主串进行匹配，此时模式串的字符是d而主串的字符是a，出现了字符不匹配的情况，此时记录模式串p的值为2，然后拿着坏字符a从模式串p位置开始向前匹配，当对比到模式串位置0的时候，发现模式串的字符是a，和坏字符能够匹配，所以此时q的值就是0，而模式串相对主串移动的位置就是p-q等于2。如图：

以此类推，最终直到模式串和主串匹配成功或者模式串移动到主串位置结束为止。

但是仅仅依靠坏字符规则有时会遇到计算效率偏低的情况，例如主串是aaaaaaaaa，模式串是baaaa，此时每一次都需要对比到模式串最后一位才能的到坏字符，然后计算结果是模式串相对主串向右移动一位，这样的效率难免会比较低，此时就要考虑另外一种规则来进行约束了。

好后缀规则

好后缀规则和坏字符规则有点类似，都是模式串按照从右向左匹配时，遇到不匹配的字符时进行相应的处理，我们看下面这张图：

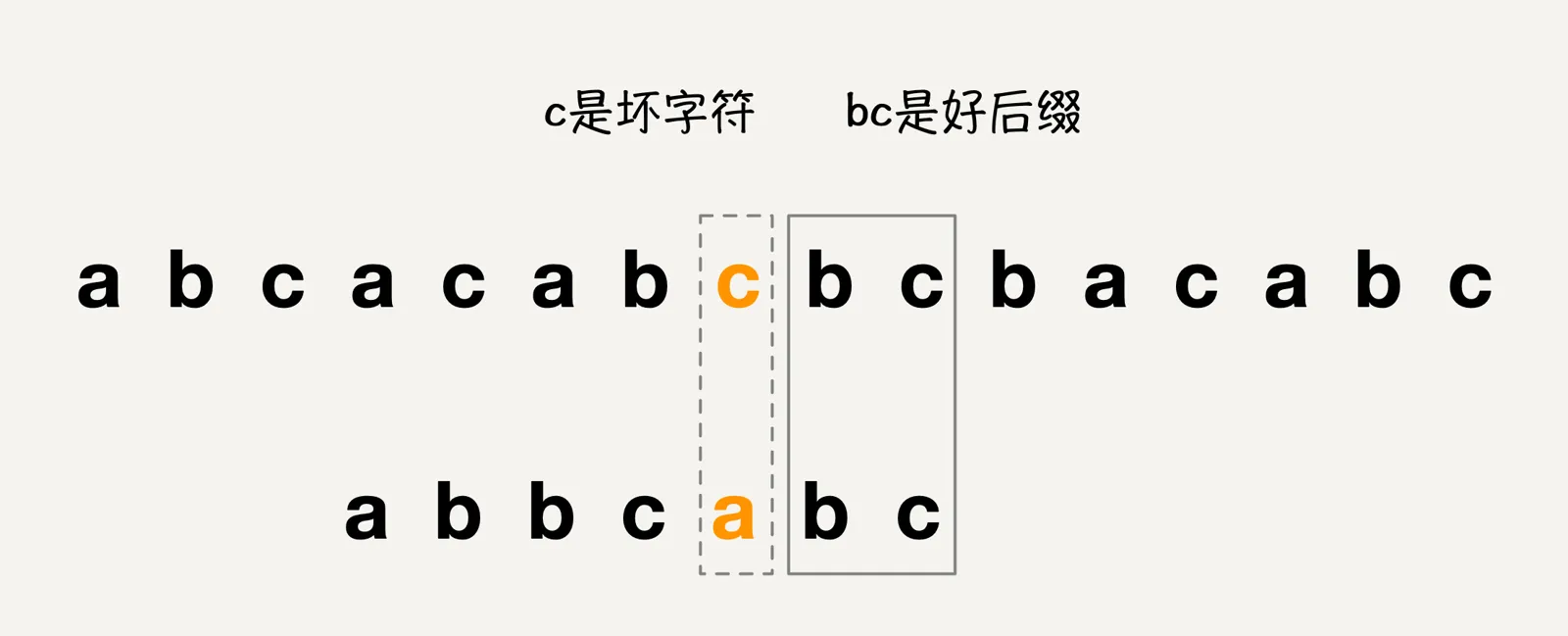
当模式串从右向左和主串进行匹配遇到上图的状态，模式串中的前两个字符和主串是匹配的，但是第三个字符进行匹配的时候，遇到了坏字符，此时如果按照坏字符规则也是可以得到相应结果，但是如果此时按照好后缀规则又怎样进行匹配呢？

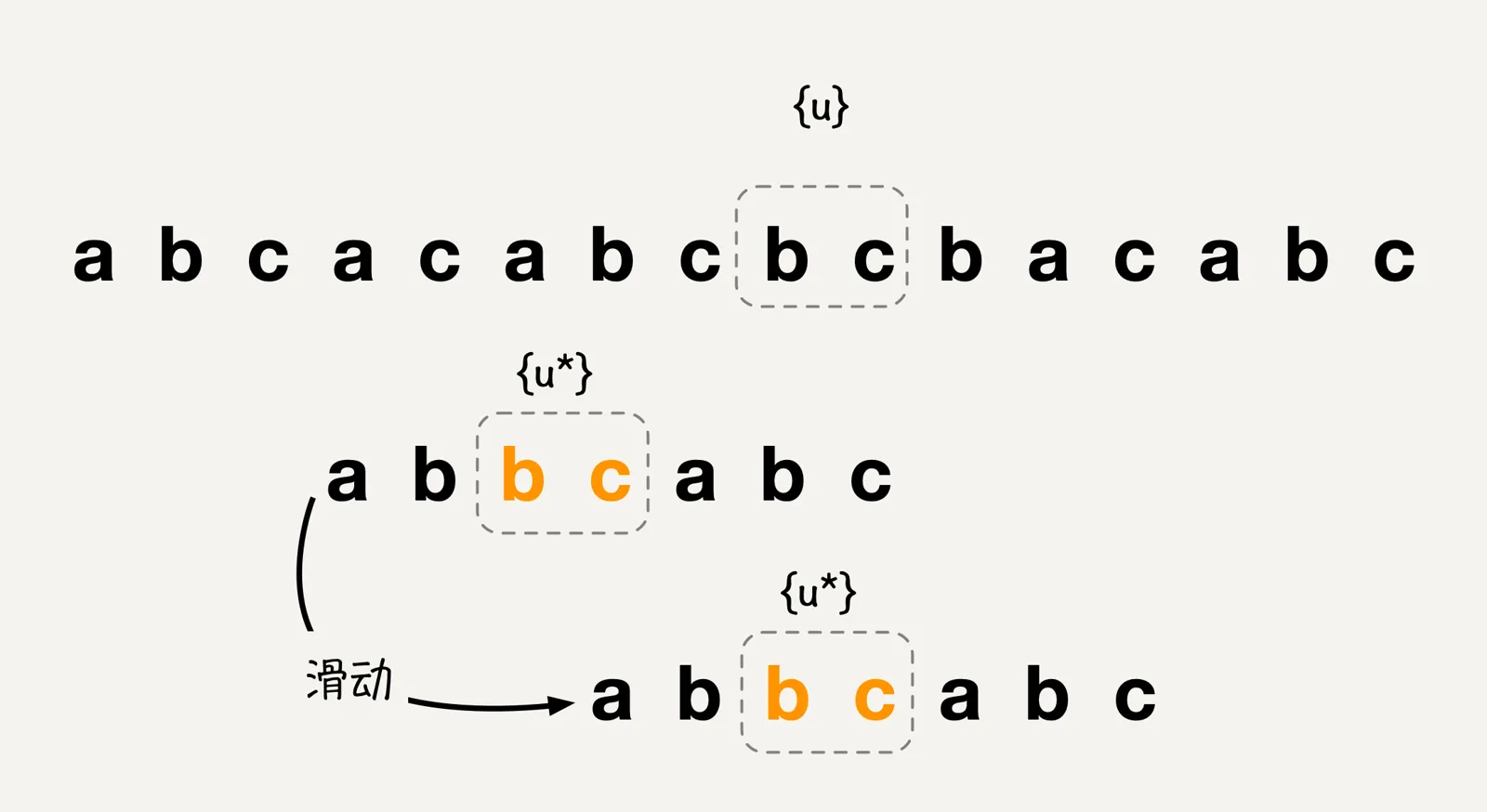
在好后缀规则下，我们把模式串中已经和主串进行匹配的字符bc叫做好后缀，记作{u}，然后我们拿着{u}从模式串与主串不匹配的位置开始向左查找，如果模式串中存在一个子串{u*}和{u}相匹配，那么我们就将模式串向右滑动到子串{u*}与主串{u}相匹配的位置，如图：

如果在模式串中找不到另外一个等于{u}的子串，那么就需要考虑直接将模式串移动到主串{u}的后面，还是移动其它指定距离呢？

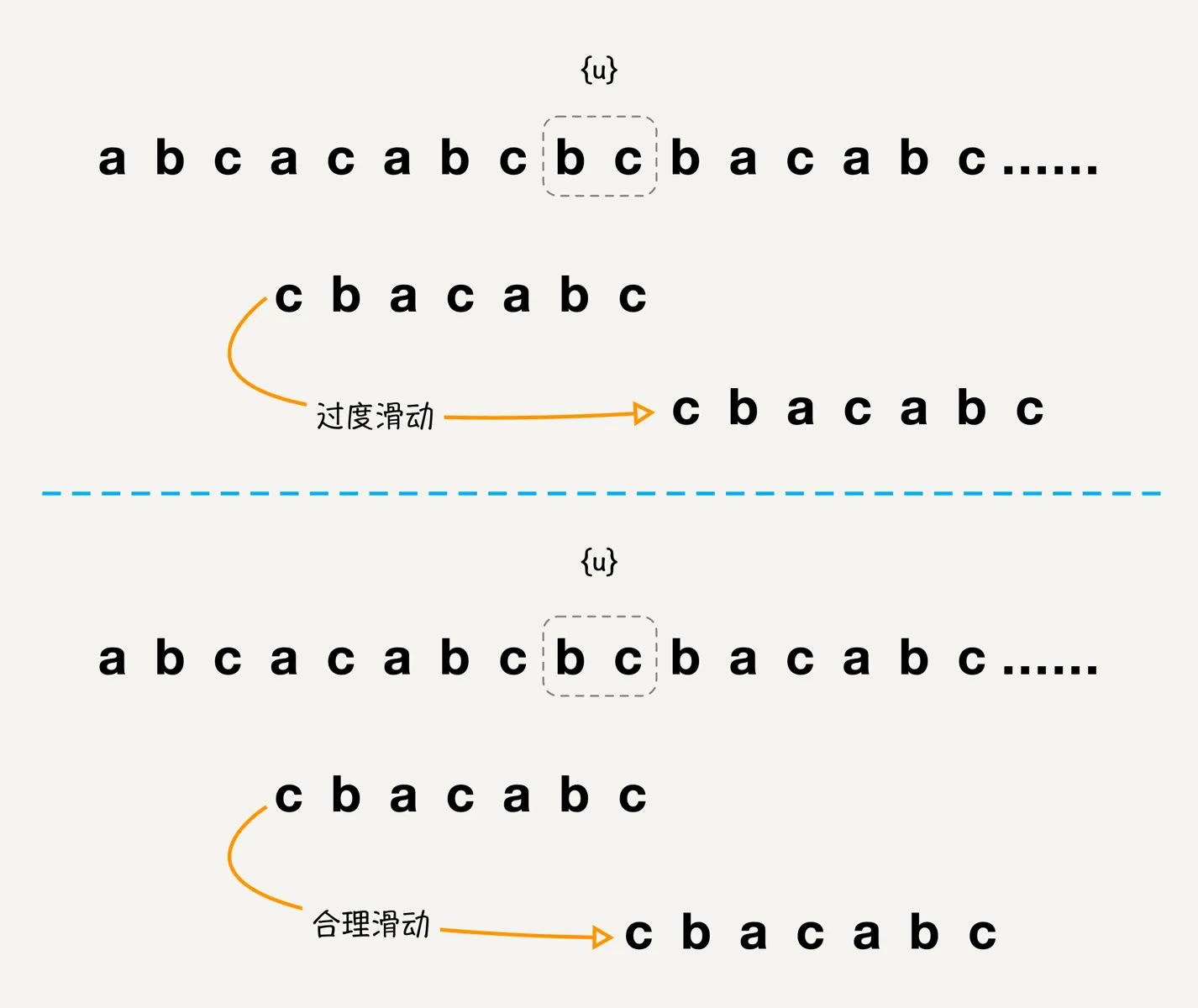
如果将模式串直接移动到主串中{u}后面，将会出现丢失匹配的情况，导致最终的匹配失效，例如下图所示例子：

如上图所示，字符串bc是好后缀，而模式串中没有找到对应的子串{u*}，此时如果模式串直接移动到好后缀bc的右边，那么就会无法正确匹配到相应子串。而如果模式串一步一步向右移动的话，只要模式串和主串{u}有重合，也是不能匹配的，因为模式串中不存在与{u}相匹配的{u*}，所以最终模式串和主串中{u}部分匹配时，才会存在完全匹配的情况。

所以当模式串中不存在与好后缀{u}向匹配的子串{u*}时，需要考察好后缀的后缀子串是否存在跟模式串的前缀子串匹配的。

这里插播一下前缀子串和后缀子串，举个例子：

已知字符串abcdefg，那么该字符串的前缀子串就是a、ab、abc、abcd、abcde、abcdef，而后缀子串就是g、fg、efg、defg、cdefg、bcefg。

思想总结

到这里，坏字符和好后缀的基本思想就讲完了，下面我们还是来做一个总结：

首先，坏字符是主串和模式串从右往左匹配的时候，遇到的第一个不匹配的字符，称为坏字符，遇到坏字符之后，解决方案是从模式串和主串第一个不匹配的位置开始，沿着模式串向左利用坏字符依次和模式串进行匹配，如果模式串中存在和坏字符匹配的，那么模式串就向右移动一定距离，使得模式串中和坏字符匹配的这个字符能够和主串的坏字符对齐；如果坏字符没有和模式串匹配，那么模式串直接移动到主串坏字符位置的右边。

而好后缀和坏字符规则类似，也是在模式串和主串从右往左匹配，遇到第一个不匹配的字符的时候，好后缀规则是拿着坏字符右侧的相匹配的好后缀和模式串中的剩余子串进行匹配，如果有匹配到对应子串，那么模式串就向右移动，使得好后缀子串能够和模式串中匹配到的子串对齐；如果好后缀没有和模式串中的剩余子串匹配，那么就要考虑好后缀的后缀子串是否跟模式串的前缀子串匹配，这里的匹配是一个比较复杂的过程。

代码实现

俗话说，talking is cheap, show me the code，那么接下来我们就来看看BM算法该如何利用代码实现。

这里我不会真正地通过代码来实现BM算法，因为我相信理解了思想，每一个人都可以实现代码，不拘束于特定的代码上，我们主要来讨论一下坏字符规则和好后缀规则的核心思想，也就是我上面思想总结中关于两个规则的讨论该如何用代码实现。

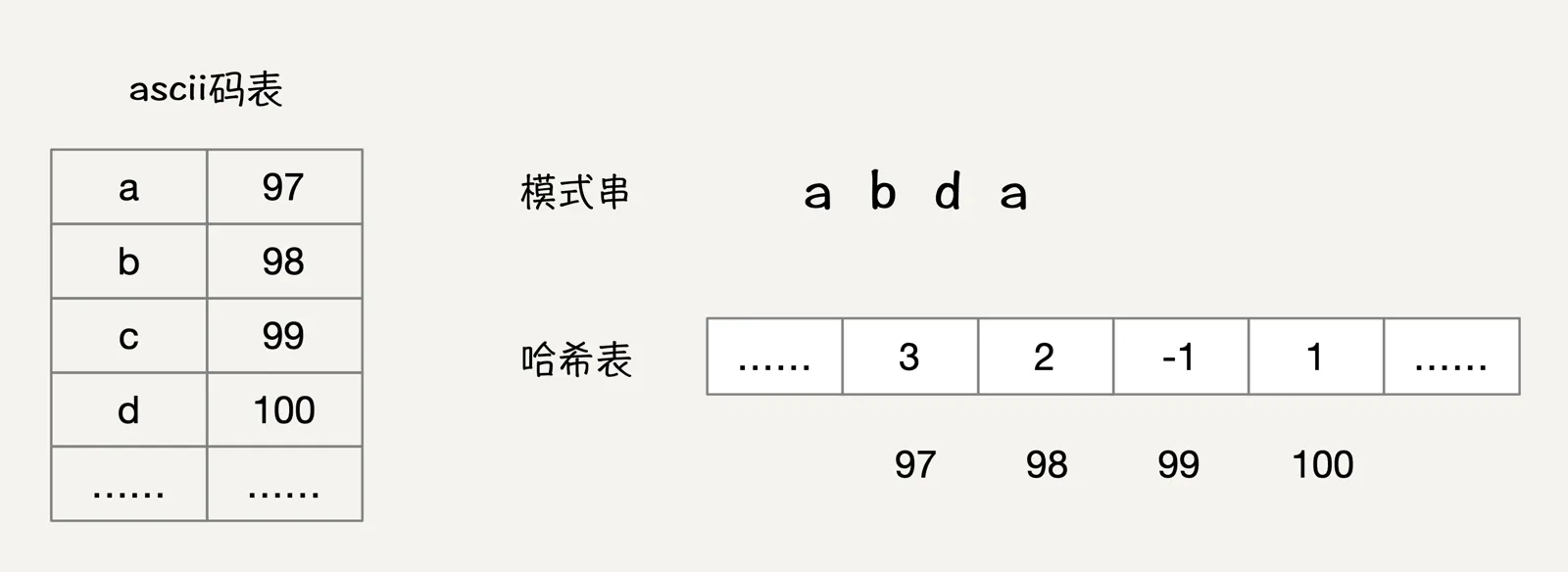
在坏字符规则中，坏字符需要和模式串中剩余子串进行匹配，找到模式串中能够和坏字符相匹配的字符位置q，然后计算模式串向右移动位数p-q，所以如果能够加速这一过程，就可以大大提高坏字符规则执行效率。这里可以考虑使用查表法来解决问题，我们假设主串和模式串中对应的字符串字符集不是很大，那么我们就可以使用大小为256的数组记录每一个字符在字符串中的位置，数组下标对应字符ascii码值，数组中存储的是该字符在模式串中的位置，注意这里如果模式串中有多个相同的字符，那么最终会取最后一个字符位置，作为该字符的位置。

如上图所示，模式串abcd对应的哈希表中下标为97记录的是最后一次字符a在模式串中的位置3，字符b和d在模式串中的位置分别被记录在哈希表下标为98和100中。

上面思想用代码实现如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

// 全局变量或成员变量
private static final int SIZE = 256; 
//b为模式串字符数组，m为模式串长度，bc为哈希表
private void generateBC(char[] b, int m, int[] bc) {
  for (int i = 0; i < SIZE; ++i) {
    bc[i] = -1; // 初始化bc
  }
  for (int i = 0; i < m; ++i) {
    int ascii = (int)b[i]; // 计算b[i]的ASCII值
    bc[ascii] = i;
  }
}

以上就是坏字符规则中最主要的模式串字符位置记录的代码实现，这里最主要的是利用哈希表记录，而哈希表的长度取决于主串和模式串中的字符集大小，所以在字符集比较大的条件下，该算法可能占用的空间会比较大。

介绍完坏字符规则之后，我们接着聊一聊好后缀的核心思想该如何实现。

好后缀的核心思想是：

• 在模式串中，查找跟好后缀匹配的另外一个子串；
• 在好后缀的后缀子串中，查找最长的能够跟模式串的前缀子串匹配的后缀子串。

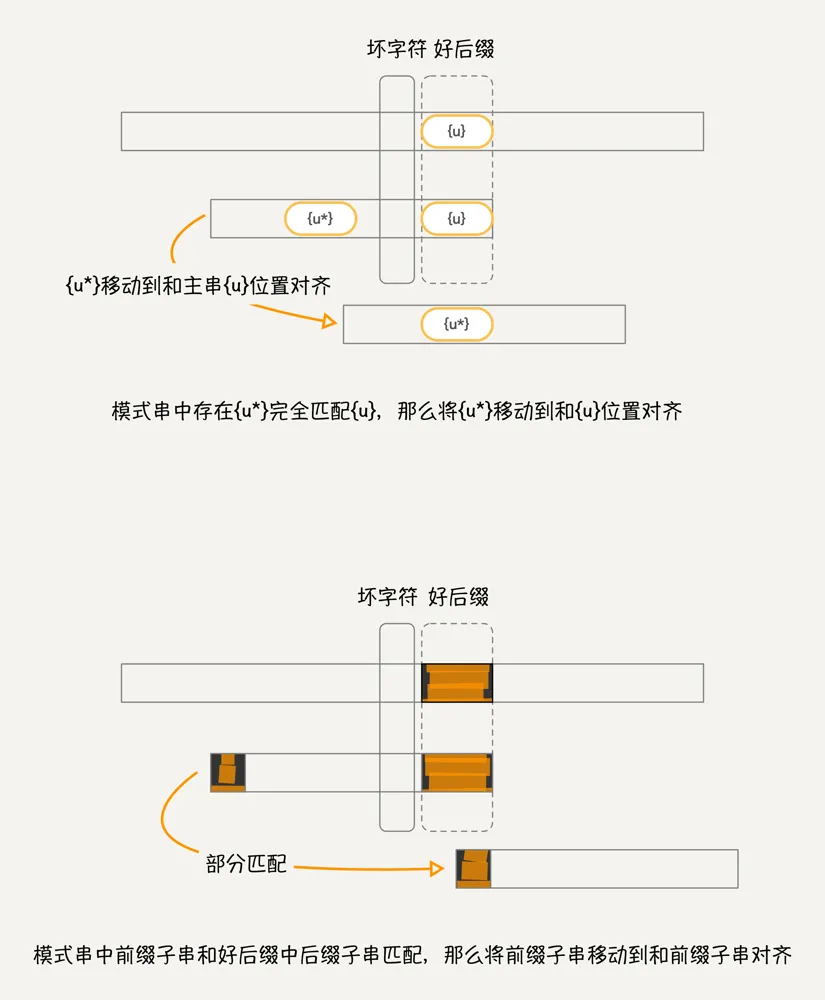
上面的意思其实就是，如果好后缀在模式串中能够找到另外一个子串匹配，那么就将该子串移动到和主串的好后缀位置对齐，如果好后缀字符串无法和模式串完全匹配，但是存在好后缀的后缀子串和模式串的前缀子串匹配，那么就将模式串部分匹配子串移动到和主串好后缀的后缀子串位置对齐。这段话可能比较难理解，可以看下面的图帮助理解：

注：部分匹配时，图中文字有误，应该为：模式串中前缀子串和好后缀后缀子串匹配，那么将前缀子串移动到好后缀后缀子串位置对齐

既然我们知道了好后缀匹配的核心思想，那么该如何设计数据结构，来预处理数据方便字符串匹配呢？

因为好后缀是模式串本身的后缀子串，所以我们可以在模式串和主串正式匹配之前，通过预处理模式串，预先计算好模式串的每个后缀子串，对应的另一个可匹配子串的位置。这里有一个比较巧妙的地方，由于好后缀是模式串本身的后缀子串，而模式串的后缀子串和长度是正相关的，也就是每一个长度可以唯一确定模式串的一个后缀子串，所以我们只需要一个长度就能得到这个长度对应的后缀子串，在这里我们引入suffix数组。

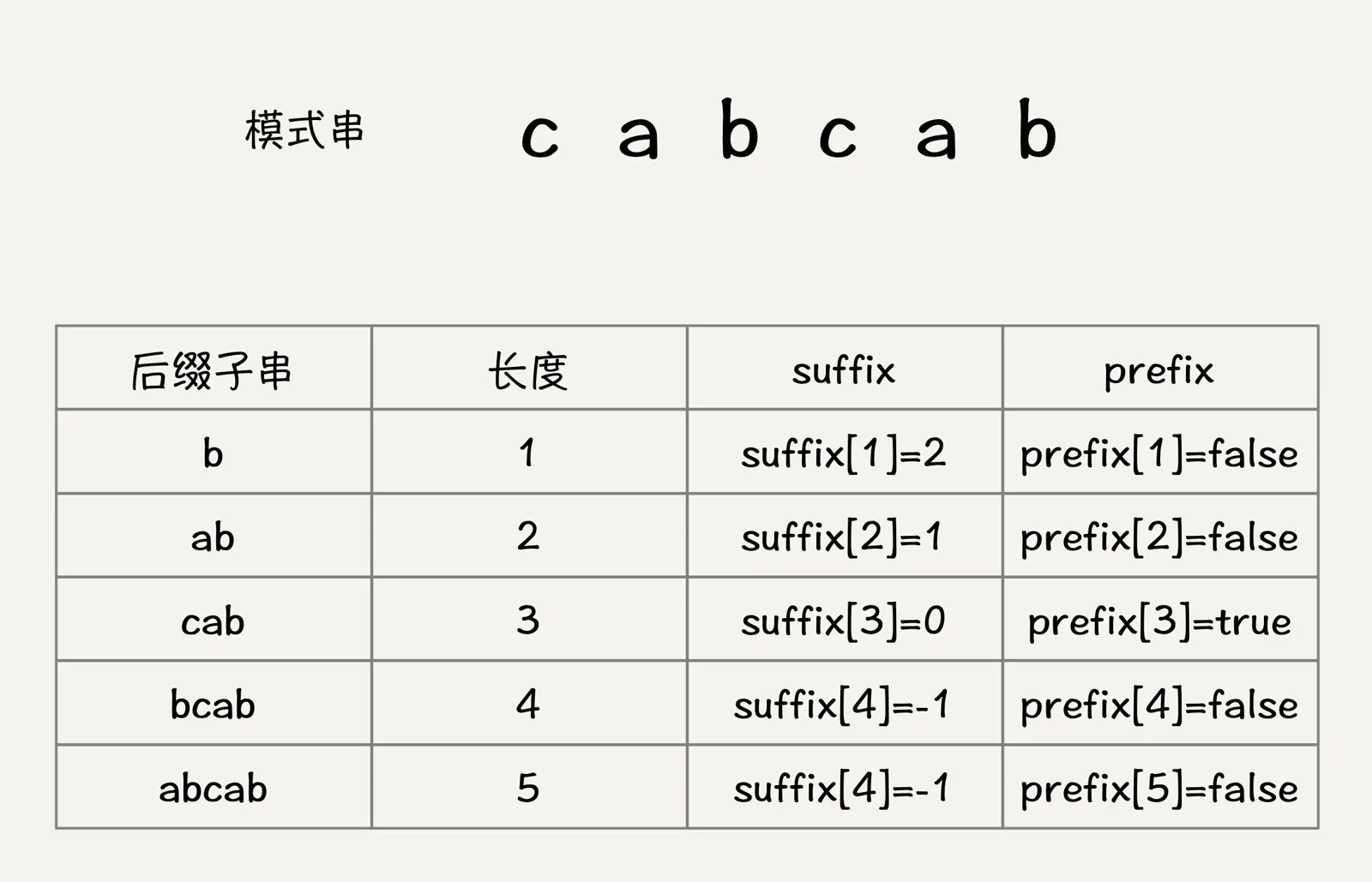
suffix数组下标k表示后缀子串的长度，下标对应的数组存储的是和当前模式串的后缀子串相匹配的子串的起始下标值。这句话可能不好理解，我们还是看图：

如上图所示，suffix数组的下标是后缀子串长度，suffix数组的值，对应的是模式串中与后缀子串匹配的子串起始位置，例如模式串中和模式串后缀子串b匹配的另外一个子串b的起始下标为2，后缀子串ab和另外一个子串ab匹配的起始下标是1，后面同理，如果出现后缀子串无法和子串匹配，那么该长度对应的数组值为-1。

如果一个模式串中出现多个子串和后缀子串匹配的情况，那么就取子串下标最大的那个值位置suffix数组的值，因为这样移动的范围最小。

仅仅依靠上述一个数组还是不能完全覆盖好后缀的两条核心思想，好后缀中当模式串中没有子串能够和好后缀进行完全匹配的时候，会去寻找好后缀的后缀子串中最长的能够和模式串的前缀子串相匹的后缀子串。所以上面的suffix数组就无法满足条件，这里就引入了另外一个boolean类型的prefix数组，来记录模式串的后缀子串是否能够匹配模式串的前缀子串。

如图所示，因为prefix是记录好后缀中的后缀子串和模式串的前缀子串能否匹配的，而好后缀其实也是属于模式串的后缀子串，所以只需要记录模式串的后缀子串和模式串的前缀子串能否匹配即可，而从suffix数组中我们可以知道，当suffix数组的值为0时，我们记录的就是该长度的后缀子串能够和该长度的前缀子串相匹配，此时设置prefix在该长度的值为true。

suffix和prefix数组的计算过程用代码实现出来就是下面这样：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

// b表示模式串，m表示长度，suffix，prefix数组事先申请好了
private void generateGS(char[] b, int m, int[] suffix, boolean[] prefix) {
  for (int i = 0; i < m; ++i) { // 初始化
    suffix[i] = -1;
    prefix[i] = false;
  }
  for (int i = 0; i < m - 1; ++i) { // b[0, i]
    int j = i;
    int k = 0; // 公共后缀子串长度
    while (j >= 0 && b[j] == b[m-1-k]) { // 与b[0, m-1]求公共后缀子串
      --j;
      ++k;
      suffix[k] = j+1; //j+1表示公共后缀子串在b[0, i]中的起始下标
    }
    if (j == -1) prefix[k] = true; //如果公共后缀子串也是模式串的前缀子串
  }
}

到此，好后缀规则也介绍完了，接下来就剩最后一个疑问，这个好后缀规则，在字符串匹配时该如何使用？

我们假设模式串和主串在匹配过程中，好后缀的长度为k，那么我们就拿着该长度在suffix数组中进行查找，如果suffix[k]!=-1，那么我们就将模式串相对于主串向右移动p-suffix[k]+1位，这里的p就是我们上面提到的坏字符在模式串中的下标。

如果suffix[k]=-1，那么说明模式串中不存在子串和好后缀完全匹配，此时就需要找prefix数组中是否存在好后缀后缀子串和模式串前缀子串匹配，这里查找规则是依次从好后缀的最长的后缀子串开始，依次在prefix数组中查找，如果查找到长度为k的子串满足prefix[k]=true，那么就可以把模式串相对于主串位置，向右移动m-k位，m表示模式串长度。

如果上面两种情况都没有从模式串中找到可以匹配好后缀的子串，以及后缀子串，那么就可以将整个模式串后移m位。

总结

到此，关于字符串匹配的三种算法都讲完了，下面我们来做一个总结。

• BF是字符串暴力匹配算法，实现起来比较简单，但是复杂度比较高。
• RK算法在BF算法的基础上，增加了哈希匹配，在主串的子串和模式串进行匹配之前，先对比两个字符串的哈希值，如果两个哈希值相同才进行字符串匹配；当然，如果选择比较复杂的哈希算法来避免哈希冲突，可能导致越界情况，所以一般都是在一定程度上允许哈希冲突来解决该问题，这里需要注意如何平衡这两个问题，毕竟如果哈希算法选择过于简单，那么该算法和BF算法没有什么区别。
• BM算法是性能比较高的单模式字符串匹配算法，其核心思想由坏字符规则和好后缀规则组成，所以如果理解了这两个规则，那么该算法的理解也就不在话下。
• 坏字符规则中需要理解什么是坏字符，以及如何利用哈希表构建对应的字符库，方便快速查找坏字符在模式串中的另外一个匹配的位置。
• 好后缀规则的实现主要通过两个数组，分别是suffix和prefix，这两个数组对应好后缀中的两条思想，分别是好后缀子串能够在模式串中找到另外一个完全匹配的子串，以及如果找不到完全匹配的子串，如何折中查找好后缀的后缀子串与模式串的前缀子串的匹配。suffix数组主要记录了模式串的后缀子串匹配到模式串中另外一个子串的位置，prefix数组则记录了模式串的后缀子串能否和模式串的同等长度的前缀子串相匹配。
• 坏字符规则占用空间大小和字符串的字符集大小有关，而好后缀规则占用空间大小主要和模式串大小相关，所以如果字符串的字符集比较丰富，那么坏字符规则不是一个好的选项。